3277. City Horizon
Farmer John has taken his cows on a trip to the city!
As the sun sets, the cows gaze at the city horizon and observe the beautiful
silhouettes formed by the rectangular buildings.
The entire horizon is represented by a number line
with n (1 ≤ n ≤ 40,000) buildings. Building i's silhouette has a base that spans
locations ai
through bi
along the horizon (1 ≤ ai <
bi ≤ 109) and has height hi (1
≤ hi
≤ 109). Determine the
area, in square units, of the aggregate silhouette formed by all n buildings.
Input. The first line contains
asingle
integer n. Each of the next n lines describes building i
with three space-separated integers: ai, bi, and hi.
Output. Print the total area, in square
units, of the silhouettes formed by all n buildings
Sample Input
4
2 5 1
9 10 4
6 8 2
4 6 3
Sample
Output
16
РЕШЕНИЕ
заметающая прямая
Анализ алгоритма
Отсортируем точки –
абсциссы начал и концов запросов по возрастанию. С каждой точкой запомним,
является ли она началом (type = 0)
или концом (type = 1) запроса, а
также высоту соответствующего ей здания. Будем последовательно обрабатывать
точки слева направо.
В мультимножестве s храним
высоты зданий, которые на данный момент уже начались, но еще не закончились.
Мультимножество будет поддерживать высоты по убыванию.
Пусть на данный момент мы
находимся в точке xi. Пусть
h – наибольшее число в
мультимножестве. Это значит, что текущее самое высокое здание имеет высоту h (которое еще не закончилось). Добавим
к площади горизонта значение (xi
– xi+1) * h. Если точка xi – начало здания, то соответствующую ей высоту добавим
в мультимножество. Если конец здания – то удалим из мультимножества его высоту.
Порядок обработки начал и концов зданий с одинаковыми абсциссами не имеет
значения.
Пример
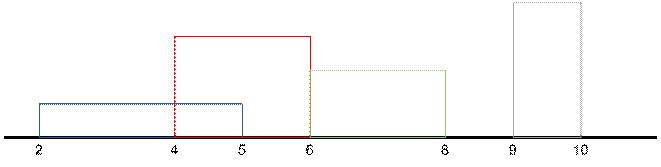
Реализация алгоритма
#include <cstdio>
#include <set>
#include <vector>
#include <algorithm>
using namespace
std;
struct node
{
int x, flag, h;
node(int x, int flag, int h) : x(x), flag(flag), h(h) {};
int operator< (const node &a) const
{
return x < a.x;
}
};
vector<node> Event;
multiset<int, greater<int> > s;
int i, n, left, right, height, last;
long long
res;
int main(void)
{
scanf("%d",&n);
for(i = 0; i < n; i++)
{
scanf("%d %d %d",&left,&right,&height);
Event.push_back(node(left,0,height));
Event.push_back(node(right,1,height));
}
sort(Event.begin(),Event.end());
res = last = 0;
for(i = 0; i < 2*n; i++)
{
int x = Event[i].x;
int type = Event[i].flag;
int h = Event[i].h;
if(!s.empty())
res += 1LL *
*s.begin() * (x - last);
if(type == 0)
s.insert(h);
else
s.erase(s.find(h));
last = x;
}
printf("%lld\n",res);
return 0;
}
Реализация при помощи дерева отрезков
#include <cstdio>
#include <cstring>
#include <set>
#include <map>
#include <vector>
#include <algorithm>
#define MAX 80010
using namespace
std;
int SegTree[4*MAX];
vector<int> a;
map<int,int> mp;
int i, n, l, r, h, len;
long long
res;
struct Building
{
int left, right, height;
} b[40010];
void Push(int
Vertex, int LeftPos, int
Middle, int RightPos)
{
if (SegTree[Vertex])
{
SegTree[2*Vertex] =
max(SegTree[2*Vertex],SegTree[Vertex]);
SegTree[2*Vertex+1]
= max(SegTree[2*Vertex+1],SegTree[Vertex]);
SegTree[Vertex] =
0;
}
}
void Add(int
Vertex, int LeftPos, int
RightPos, int Left, int
Right, int x)
{
if (Left > Right) return;
if ((LeftPos == Left) && (RightPos == Right))
SegTree[Vertex] =
max(SegTree[Vertex],x);
else
{
int Middle = (LeftPos + RightPos) / 2;
Push(Vertex,LeftPos,Middle,RightPos);
Add(2*Vertex,
LeftPos, Middle, Left, min(Middle,Right), x);
Add(2*Vertex+1,
Middle+1, RightPos, max(Left,Middle+1), Right, x);
}
}
long long
Count(int Vertex, int
LeftPos, int RightPos)
{
if (LeftPos == RightPos)
return 1LL * SegTree[Vertex] * (a[LeftPos+1] -
a[LeftPos]);
else
{
int Middle = (LeftPos + RightPos) / 2;
Push(Vertex,LeftPos,Middle,RightPos);
return Count(2*Vertex, LeftPos, Middle) +
Count(2*Vertex+1, Middle+1, RightPos);
}
}
int main(void)
{
scanf("%d",&n);
memset(SegTree,0,sizeof(SegTree));
set<int> s;
for(i = 1; i <= n; i++)
{
scanf("%d %d %d",&b[i].left,&b[i].right,&b[i].height);
s.insert(b[i].left); s.insert(b[i].right);
}
len = s.size();
a.resize(len+2);
copy(s.begin(),s.end(),a.begin()+1);
for(i = 1; i <= len; i++) mp[a[i]] = i;
for(i = 1; i <= n; i++)
Add(1,1,len,mp[b[i].left],mp[b[i].right]-1,b[i].height);
res = Count(1,1,len);
printf("%lld\n",res);
return 0;
}